SISTEM BILANGAN
A.
PENGERTIAN SISTEM BILANGAN
Sistem bilangan adalah sebuah
kumpulan dari simbol yang menjelaskan ulang sebuah bilangan. Numerik berbeda
dengan angka. Simbol “6″, “enam” and “VI” adalah numerik yang berbeda, tetapi
menjelaskan ulang sebuah angka yang sama. Sistem bilangan ini biasa digunakan
pada komputer untuk berkomunikasi dan berbagi daya dengan komputer lain.
Sistem
Digital adalah suatu sistem yang berfungsi untuk mengukur suatu nilai atau
besaran yang bersifat tetap atau tidak teratur dalam bentuk diskrit berupa
digit digit atau angka angka .Biasanya sebelum mempelajari lebih dalam tentang
sistem digital pertama pasti kita akan mempelajari yang namanya Sistem
Bilangan ,ada 4 jenis sistem bilangan yaitu biner ,oktal ,desimal ,hexadesimal
.
Bilangan
Oktal adalah bilangan yang hanya punya basis 8 atau bilangan basis 8 , yaitu
0,……,7. Bilangan Desimal adalah bilangan yang hanya punya basis 10 atau
bilangan basis 10 ,yaitu 0,…….9. Bilangan Hexadesimal adalah bilangan yang
hanya punya basis 16 atau bilangan basis 16 ,yaitu 0,……..9 ,A ,B ,C ,D ,E ,F
(A=10 ,B=11 ,C=12 ,D=13 ,E=14 ,F=15)
Konversi
Bilangan adalah mengubah suatu sistem bilangan menjadi sistem bilangan
lain.
AMERICAN STANDARD CODE FOR INFORMATION INTERCHANGE
(ASCII)
dikonversi menjadi 8 digit angka 0 dan 1 (8-bit)
ASCII-8 memiliki 256 karakter, dari nomor 0 s.d 255
• BIT=binary
digit (sebuah angka nol atau
satu)
• 1 BYTE =
1 karakter (misalnya berds. ASCII-
8, 1 byte=8 bits)
• 1
Kilobyte (KB) = 1024 bytes
• 1
Megabyte (MB) = 1024 KB
• 1 Gigabyte
(GB)= 1024 MB
• 1
Terabyte (TB) = 1024 GB
1.
BITS DAN BYTES
Cara termudah untuk memahami bit adalah
untuk membandingkan mereka untuk sesuatu yang Anda tahu: digit. Sebuah angka
tersebut adalah satu tempat yang dapat menampung numerik nilai antara 0 dan 9
Digit biasanya digabungkan bersama-sama dalam kelompok untuk membuat angka yang
lebih besar.
Misalnya, 6357 memiliki empat digit
7 adalah mengisi "tempat 1s,"
5 adalah mengisi tempat 10s
3 adalah mengisi tempat 100
6 adalah mengisi 1.000 s tempat
(6 * 1000) + (3 * 100) + (5 * 10) + (7 *
1)
= 6000 + 300 + 50 + 7
= 6357
Komputer terjadi beroperasi menggunakan
dasar-2 sistem nomor, juga dikenal sebagai biner sistem nomor (seperti nomor
basis-10 Sistem ini dikenal sebagai sistem bilangan desimal). Alasan komputer
menggunakan basis-2 sistem karena itu membuat lebih mudah untuk menerapkannya
dengan teknologi elektronik saat ini.
Dengan 8 bit dalam byte, Anda dapat
mewakili 256
nilai mulai dari 0 sampai 255
0 = 00000000
1 = 00000001
2 = 00000010
...
254 = 11111110
255 = 11111111
Contoh:
a. 1243 = (1 X 10 3
) + (2 X 10 2 ) + (4 X 10 1 ) + (3 X 10 0 )
=
1000 + 200 + 40 + 3
b. 752,91 = (7 X 10 2 ) + (5 X 10 1 ) + (2 X 10 0 ) + (9 X
10 1) + (1 X 10 2)
= 700 + 50 + 2 + 0,9 + 0,01
a. Biner
Bilangan
Biner adalah bilangan yang hanya punya basis 2 atau bilangan basis 2 ,yaitu 0
dan 1, Sistem bilangan biner
modern ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem
bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Hampir semua sistem digital menggunakan
sistem bilangan biner sebagai dasar sistem bilangan dari operasinya, meskipun
sistem-sistem bilangan lain sering digunakan secara bersama-sama dengan biner.
Dengan menggunakan 2 level yang ada pada sistem biner maka sangatlah mudah
untuk mendesain rangkaian – rangkaian elektronik yang akurat dibandingkan
dengan menggunakan 10 level yang ada pada sistem desimal.
Dalam sistem biner, hanya ada 2 simbol atau digit yaitu 0
dan 1 yang dikenal juga dengan system basis-2. Sistem biner ini dapat digunakan
untuk menyatakan setiap kuantitas yang dapat dinyatakan dalam desimal atau
sistem bilangan yang lainnya.
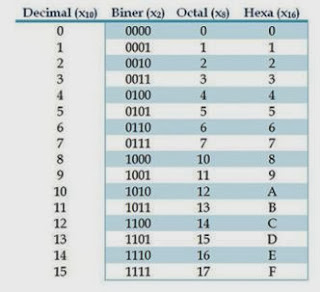
Tabel berikut menunjukkan urutan hitungan pada system
bilangan biner.
Ada beberapa konversi bilangan pada bilangan
biner, antara lain :
·
Biner ke Oktal
Caranya
mudah ,kita hanya menyekatnya atau mengelompokkan berisi 3 bit bilangan ,dalam
bentuk bilangan oktal ,111 =
4+2+1 = 7 ,sistem oktal ini disebut sistem 421.
Contohnya
110011010(2) = 110 011 010 = 4+2+0 0+2+1
0+2+0 = 632(8)
·
Biner ke Desimal
Kita
hanya tinggal mengalikan setiap bitnya dengan 2n ,n = posisi bit ,MSB berarti
pangkatnya paling besar , sedangkan
LSB pangkatnya paling kecil atau = 0, lalu hasilnya dijumlahkan .
Contoh
:
110011010(2) = (1×28) + (1×27) + (0×26) +(0×25) + (1×24) +
(1×23) + (0×22) + (1×21) +(0×20) = 256 + 128
+ 0 +
0 + 16 +
8 + 0
+ 2 + 0 = 410(10)
·
Biner ke Hexadesimal
Caranya
mudah ,kita hanya menyekatnya atau mengelompokkan berisi 3 bit bilangan , alam bentuk bilangan
oktal ,1111 = 8+4+2+1 = 15/F , sistem
hexadesimal ini disebut sistem 8421.
Contoh
:
10110011010(2) = 1101 1001 1010 = 8+4+0+1
8+0+0+1 8+0+2+0 = 13 9 10 = D9A(16)
b.
Oktal
Oktal adalah sebuah sistem bilangan berbasis delapan.
Simbol yang digunakan pada sistem ini adalah 0,1,2,3,4,5,6,7. Konversi Sistem
Bilangan Oktal berasal dari Sistem bilangan biner yang dikelompokkan tiap tiga
bit biner dari ujung paling kanan (LSB atau Least Significant Bit).
Ada cara lain
untuk "menghitung" selain desimal dan sistem biner. Salah satu contoh
adalah
-
Oktal adalah sistem
penomoran menggunakan pertama 8
angka mulai dari 0-20 angka pertama
dalam sistem oktal adalah: 0,1,2,3,4,5,6,7,10,11,12,13,14,15,16,17, 20,21,22,23
-
Karena ada 8 angka
dan 8 pola yang dapat dibentuk oleh 3 bit, sejumlah oktal tunggal mungkin digunakan
untuk mewakili kelompok 3 bit
-
Oleh karena itu,
bilangan biner di atas mungkindiwakili oleh: 51.278 dalam bentuk oktal
Ada beberapa
konversi bilangan pada bilangan octal , antara lain :
·
Oktal ke Desimal
Kita
hanya tinggal mengalikan angka paling kiri dengan 8n , n adalah jumlah pangkaat tertinggi. MSB berarti pangkatnya
paling besar sedangkan LSB pangkatnya paling kecil atau = 0, lalu hasilnya
dijumlahkan .
Contoh
:
678(8) = 6×82 7×81 8×80 = 6×64
+ 7×8 + 8×1 = 384 + 56 + 8 = 440(10)
·
Oktal ke Biner
Pada
konversi bilangan oktal ke biner ini maksimal hanya angka misalnya 777(8) yang dapat langsung dikonversikan
kebiner dengan cara sekat 7 = 111 , 7 = 111 , 7 = 111 jadi 777(8) =111111111(2)
,jika 777 keatas sudah tidak bisa
menggunakan cara ini ,harus diubah kedesimal dahulu baru bisa langsung ke
biner.
Contoh
:
653(8) = ( dengan cara sekat langsung karena tidak ada angka
yang >7 )
653(8) = 6 = 110 ,5 = 101 , 3 = 011,,,Jadi 653(8) =
110101011(2)
678(8) = ( langkah pertama harus dikonversikan terlebih
dahulu ke desimal )
678(8) = 6×82 7×81 8×80 = 6×64 + 7×8 + 8×1 = 384
+ 56 + 8 = 440(10)
440(10) = ( langkah kedua langsung mengubahnya kebiner )
440(10) = 440:2=220 sisa 0
220:2=110 sisa 0
110:2=55 sisa 0
55:2=27 sisa 1
27:2=13 sisa 1
13:2=6 sisa 1
6:2=3 sisa 0
3:2=1 sisa 1
1:2=0 sisa 1
dibaca dari bawah keatas ,jadi 440(10) = 110111000(2)
Jadi , 678(8) = 110111000(2)
·
Oktal ke Hexadesimal
Caranya
kita harus mengubahnya ke bilangan desimal dahulu baru dari desimal kiata ubah
ke hexadesimal .
Contoh
:
678(8) = 6×82 7×81 8×80 = 6×64 + 7×8 + 8×1 = 384
+ 56 + 8 = 440(10)
440(10) = 440:16= 27 sisa 8
27:16= 1 sisa 11/B
1:16= 0 sisa 1
dibaca dari bawah keatas Jadi, 440(10) = 1B8(16)
Jadi ,hasil dari
678(8) = 1B8(16)
c. Desimal
Sistem desimal tersusun atas 10 angka atau simbol, yang dikenal dengan digit. Ke-10 simbol ini adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Sistem desimal juga disebut sistem basis-10, karena mempunyai 10 digit. Kenyataannya, kata ”digit” adalah kata latin yang berarti ”jari-jari”.
Sistem
desimal adalah suatu sistem nilai posisional di mana nilai
dari suatu digit tergantung kepada posisinya. Misalnya perhatikanlah bilangan
desimal 634 ini artinya digit 4 sesungguhnya menyatakan 4 satuan. 3 menyatakan
3 puluhan dan 6 menyatakan 6 ratusan. Ringkasnya, 6 merupakan yang paling
berbobot dari ketiga digit, dikenal sebagai Most Significant Digit (MSD). 4
bobotnya paling kecil dan disebut Least Significant Digit (LSD). Perhatikan
contoh lain, 75.25. Bilangan ini sesungguhnya sama dengan tujuh puluh plus lima
satuan plus dua persepuluh plus
Ada beberapa konversi bilangan pada
bilangan desimal , antara lain :
·
Desimal ke Biner
Kita
hanya tinggal membagi angka desimalnya dengan angka 2 dan hasilnya tidak ada
koma ,tapi kita tulis saja berapa sisanya .
Contoh
:
440(10) = 440:2=220 sisa 0
220:2=110 sisa 0
110:2=55 sisa 0
55:2=27 sisa 1
27:2=13 sisa 1
13:2=6 sisa 1
6:2=3 sisa 0
3:2=1 sisa 1
1:2=0 sisa 1
dibaca dari bawah keatas ,jadi 440(10) = 110111000(2)
·
Desimal ke Oktal
Kita
hanya tinggal membagi angka desimalnya dengan angka 8 dan hasilnya tidak ada
koma ,tapi kita tulis saja berapa sisanya.
Contoh
:
440(10) = 440:8= 55 sisa 0
55 :8= 6 sisa 7
7 :8= 0 sisa 7
dibaca dari bawah keatas ,jadi 440(10) = 770(8)
·
Desimal ke Hexadesimal
Caranya
yaitu hanya tinggal membagi angka desimalnya dengan angka 16 dan hasilnya tidak
ada koma ,tapi kita tulis saja berapa sisanya.
Contoh
:
440(10) = 440:16= 27 sisa 8
27:16= 1 sisa 11/B
1:16= 0 sisa 1
dibaca dari bawah keatas Jadi, 440(10) = 1B8(16)
d. Hexadesimal
Heksadesimal adalah sebuah sistem
bilangan yang menggunakan 16 simbol. Berbeda dengan sistem bilangan desimal,
simbol yang digunakan dari sistem ini adalah angka 0 sampai 9, ditambah dengan
6 simbol lainnya dengan menggunakan huruf A hingga F. Sistem bilangan ini
digunakan untuk menampilkan nilai alamat memori dalam pemrograman komputer.
Konversi Sistem Bilangan Hexadesimal berasal dari Sistem bilangan biner yang
dikelompokkan tiap 4 bit biner dari ujung paling kanan (LSB atau Least
Significant Bit).
Ada beberapa konversi bilangan pada
bilangan desimal , antara lain :
·
Hexadesimal ke Biner
Kita
hanya tinggal menyekat 1 bilangan Hexadesimal lalu mengubahnya ke biner.
Contoh
:
B4645(16) = B 4 6 4
5 = 1011 0100 0110 0100 0101(2)
·
Hexadesimal ke Desimal
Kalikan setiap bit
bilangannya dengan 16n , n adalah nilai pangkat tertinggi MSB berarti
pangkatnya paling besar sedangkan LSB pangkatnya paling kecil atau = 0,
hasilnya lalu jumlahkan .
Contoh
:
1B8(16) = 1×162+Bx161+8×160
=256+176+8=440(10)
·
Hexadesimal ke Oktal
Bilangan Hexa tidak
bisa langsung dikonversikan ke oktal ,ubah dulu ke desimal lalu dari desimal
bisa langsung dikonversikan ke oktal.
Contoh
:
1B8(16) = 1×162+Bx161+8×160 =256+176+8=440(10)
440(10) = 440:8= 55 sisa 0
55 :8= 6 sisa 7
7 :8= 0 sisa 7
Jadi , 1B8(16) = 770(8)






Komentar
Posting Komentar